October 28, 2025
Causal Claims
Today
1. Introduction to Causality
- What is causality?
- Counterfactuals
- Potential Outcomes
A Problem in Politics
Why Causality?
Why descriptive claims matter:
descriptive claims appear in diagnostic settings:
- people attempt to convince you that there is a “problem” in need of fixing.
“Political polarization has gotten worse over time in the US”
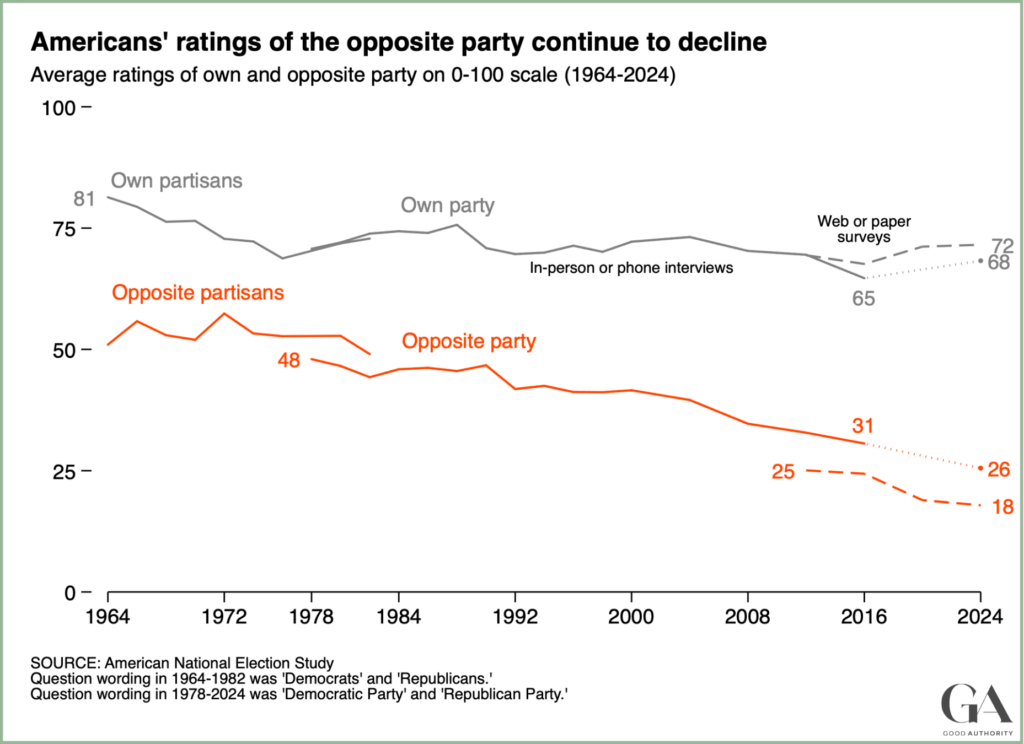
Why causality?
When people give justifications to act or think a particular way:
causal claims appear in support of prescriptive claims: claims about consequences of actions
Typically speaks to:
- what caused the problem that needs to be fixed?
- what action will produce the solution/better outcome?
Causal claims answer causal questions
-
What are the causes of effects?
Want to explain something specific that has happened/we observe (the effect). Seek to attribute a cause for something we observe. “There is a problem. How did we get here?”
- Why did Russia invade Ukraine?
- Why is housing expensive in Vancouver?
- Why has political polarization increased?d
Causal claims answer causal questions
-
What are the effects of causes?
We want to know what happens if we do some action or some action (the cause) happens. This is about the consequences of some action. “If we take this action, will it solve the problem?”
- Has BC’s housing speculation tax reduced housing prices?
- What are the effects of restricting gun ownership on gun violence?
- Does abstaining from social media reduce political polarization?
Two ways of asking causal questions
Looking at effects of causes versus causes of effects leads to different approaches to scientific investigation
causes of effects \[\textrm{?} \xrightarrow{} \textrm{effect}\]
effects of causes \[\textrm{cause} \xrightarrow{} \textrm{?}\]
Effects of causes? Causes of effects?
Effects of causes? Causes of effects?
Why Causality?
Causal claims linked to reasons given for what we should do
We need to know:
- what do we mean by causality?
- what kind of causal claims are we talking about? (effects of causes, causes of effects)
- when and why can we see “evidence” for causality, when in fact there is none? (failure of weak severity)
- what tools can we use to test causal claims with strong severity? (we know and can check assumptions)
What is causality?
What is causality?
all causal claims are a combination of (at least) two specific descriptive claims
- sometimes these descriptive claims are made explicit, typically they are implied.
- means that: any possible issues we saw with evidence for descriptive claims can occur with causal claims
What is causality?
Homelessness increased in Canadian cities because of a Federal government headed by Justin Trudeau.
- What are the two descriptive claims in this causal claim?
What is causality?
And we’re also straightening out our cities. You know, Washington D.C., our beautiful capital, was a, a killing mess. People getting killed all the time. It was very high crime. And we sent in our National Guard … And now it’s a very safe, now it’s considered a very safe. The crime is down to almost nothing. - Donald Trump
- What is the main causal claim?
- What are the two descriptive claims in this causal claim?
What is causality?
The descriptive claims embedded in causal claims are of a specific type:
- One is a claim about how the world actually is (factual)
- One is a claim about how the world would be, if something were changed (counterfactual)
counterfactuals are the key to causality
What is causality?
And we’re also straightening out our cities. You know, Washington D.C., our beautiful capital, was a, a killing mess. People getting killed all the time. It was very high crime. And we sent in our National Guard … And now it’s a very safe, now it’s considered a very safe. The crime is down to almost nothing. - Donald Trump
- What is the main causal claim? (on the board)
- What are the two descriptive claims in this causal claim? (on the board)
Counterfactuals
Causality is Counterfactual
What does that mean?
Counterfactuals and Causality:
counterfactuals: are the way world would be if events had transpired differently (other than what actually took place).
- imagine an “alternate universe” or “alternate timeline”
contrasts to what is factual: the way the world is, given the events that have taken place.
Spoiler Warning!
Counterfactuals:
If Gwyneth Paltrow’s character…
catches the train then she catches her boyfriend cheating, and dumps him
does not catch the train then she does not catch her boyfriend cheating, and stays with him
In reality, only one of these possibilities can happen. If (a) happens, it is factual, (b) is counterfactual
An exercise
“Exposure to social media increases political polarization.”
In the lead-up to the 2025 Canadian Election, platforms owned by Meta (Facebook, Instagram, WhatsApp) blocked users access to content from Canadian news organizations while simultaneously ending fact-checking (source). This “enabled hyper-partisan content to dominate in the absence of balanced media coverage.”
“causal variable”: exposure to social media during the election
outcome variable: political polarization \(\to\) willingness to go on a date with someone who supports an opposing political party.
An exercise
“Exposure to social media increases political polarization.”
Think and write…
Imagine: If you used social media during the election, would you be willing to go on a date with someone who supported a rival political party?
Imagine: If you did not use social media during the election, would you go on a date with someone who supported a rival political party?
Take this survey
An exercise
Which of these is factual? Which is counterfactual?
\(1.\) If you used social media during the election, would you go on a date with someone voting for a rival political party?
\(2.\) If you did not social media during the election, would you go on a date with someone voting for a rival political party?
- It depends: If you actually used social media, then \(1\) is factual (\(2\) is counterfactual); If you didn’t actually use social media, then \(2\) is factual (\(1\) is counterfactual)
Potential Outcomes
Counterfactuals can be described with potential outcomes:
If \(X\) is a variable for a suspected cause (using social media) and \(Y\) is a variable for what is possibly affected (dating rival partisan)…
then potential outcomes are the values of \(Y\) that a specific case (\(i\)) would take for the different possible values of \(X\) (factual and counterfactual):
- If you used social media during the election, would you go on this date?
- If you did not use social media during the election, would you go on this date?
potential outcomes notation:
Where \(i\) corresponds to a specific case (e.g., you, Gwyneth Paltrow)
\(\text{Use Social Media}\) (\(X\)) is the causal variable (and can take different values, e.g. \(yes, no\)), then the potential outcomes of \(\text{Date across party lines}\) (\(Y_i\)) are:
\[\text{Date across party lines}_{i}(\text{Social media} = yes),\\ \text{Date across party lines}_i(\text{Social Media} = no)\]
For person \(i\), \(\text{Social Media}\) can only ever be \(yes\) or \(no\): one potential outcome is factual (it will happen), while the other will remain \(\color{red}{\textbf{counterfactual}}\) (it won’t happen)
\(^*\) Note, I will use \(\color{red}{red}\) to indicate counterfactual potential outcomes
Potential Outcomes
\(\mathrm{Love \ Life _{Gwyneth} (Catches \ the \ train )}\) \(= \mathrm{Dump \ cheating \ BF}\)
\(\mathrm{Love \ Life _{Gwyneth} (Doesn't \ catch \ the \ train )}\) \(= \mathrm{Stay \ with \ cheating \ BF}\)
We only will observe one of these two possibilities. But both could potentially have happened.
Potential Outcomes
For any supposed causal variable \(X\), and affected variable \(Y\), and case \(i\), we denote potential outcomes as:
\[Y_i(X = ?)\] What would the outcome \(Y\) for person/case \(i\) have been if \(X\) took on some value \(?\)
Draw potential outcomes on the board
Potential Outcomes: Caveat
In our example:
- We are only imagining, as if omniscient, what you would do in the alternate universe where you did(did not) consume political information on social media
- Potential outcomes are what you actually would do in that alternate universe.
Even if we don’t know whether you’d go on a date with a supporter of a rival party if you did(did not) use social media, we can imagine that there is potential outcome of what you would have done…
What do counterfactuals have to do with causality????
Causal Claims
Recall that causal claims are about how some shifting some factor changes something outcome…
Counterfactuals and Causality:
counterfactual causality
We can say that \(Y\) changes because of \(X\) only if, for case \(i\), \(Y_i(X = 1) \neq Y_i(X = 0)\):
- \(X\) causes \(Y\) if case \(i\) would have behaved (\(Y\)) differently (than it did factually) in the (counterfactual) alternate universe where everything was the same except \(X\) was changed.
REVISIT THE BOARD
Example:
Counterfactuals Example
And we’re also straightening out our cities. You know, Washington D.C., our beautiful capital, was a, a killing mess. People getting killed all the time. It was very high crime. And we sent in our National Guard … And now it’s a very safe, now it’s considered a very safe. The crime is down to almost nothing. - Donald Trump
- What is the “case”?
- What is the variable for the “cause”? What is the variable for the “effect”?
Counterfactuals Example
And we’re also straightening out our cities. You know, Washington D.C., our beautiful capital, was a, a killing mess. People getting killed all the time. It was very high crime. And we sent in our National Guard … And now it’s a very safe, now it’s considered a very safe. The crime is down to almost nothing. - Donald Trump
- What are the potential outcomes implied by the causal claim? (return to board)?
- Which is factual? What is counterfactual?
Counterfactuals and Potential Outcomes
Trump’s causal claim (implicitly): “National Guard deployment reduced murders in Washington, DC.”
Trump’s counterfactual claim: “If there had been no National Guard, DC would have had more murders.”
Counterfactual claim implies two potential outcomes:
- Number of murders in DC in the past 2 months in the presence of the National Guard: \(\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard})\)
- Number of murders in DC in the past 2 months in the absence of the National Guard \(\color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})}\)
Counterfactuals and Potential Outcomes
If Trump’s causal claim is true (“National Guard deployment reduced murders in Washington, DC.”), which should be true?
\[\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard}) < \color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})} \tag{1}\]
\[\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard}) > \color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})} \tag{2}\]
\[\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard}) = \color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})} \tag{3}\]
Counterfactuals and Potential Outcomes
And we’re also straightening out our cities. You know, Washington D.C., our beautiful capital, was a, a killing mess. People getting killed all the time. It was very high crime. And we sent in our National Guard … And now it’s a very safe, now it’s considered a very safe. The crime is down to almost nothing. - Donald Trump
Implies:
\[\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard}) < \color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})}\]
Counterfactuals and Potential Outcomes
If the claim is that “National Guard deployment reduced murders in Washington, DC.”, or
\[\textrm{Murders}_{\textrm{DC}}(\textrm{Nat'l Guard}) < \color{red}{\textrm{Murders}_{\textrm{DC}}(\textrm{No Nat'l Guard})}\]
What kinds of evidence would help assess whether this claim is true?
Conclusion:
Causality is counterfactual
- this is not a simple, intuitive way of thinking
- this complicates providing evidence
We will see:
- problems: what can go wrong with evidence for causal claims
- tools: possible solutions for these problems
- severity: what must we assume for these tools to work?