1. Fundamental Problem of Causal Inference

• independent/dependent variables
• solutions

2. Correlation

• what is it?
• problems with correlation
• Random association

If we identify polarization as a problem, addressing it requires understanding what are its causes.

View this post on Instagram

A post shared by Kate Snow (@tvkatesnow)

Social Media and Polarization:

Claim: “Getting political information social media increases political polarization.”

Evidence for this claim?

• outcome/dependent variable: US has affective polarization
• independent variable: US has widespread social media news consumption

Independent/Dependent Variables

Independent variable:

The variable capturing the alleged cause in a causal claim.

• often denoted as \(X\)

Dependent variable:

The variable capturing the alleged outcome (what is affected) in a causal claim.

• often denoted as \(Y\)

Potential Outcomes are the values of dependent variable a case would take if exposed to different values of the independent variable

Dependent Variable: Polarization

Independent Variable: Polarization

Even if social media use didn’t increase polarization…

Could we see this evidence (US has both social media use and polarization)?

• If we want to find the cause of polarization, starting from case of high polarization like the US is selection on dependent variable

Selection on the Dependent Variable

when attempting to provide evidence for causal claims, selectively observing cases based on the outcome they experience

• two problems \(\to\) absence of weak severity

Selection on the Dependent Variable

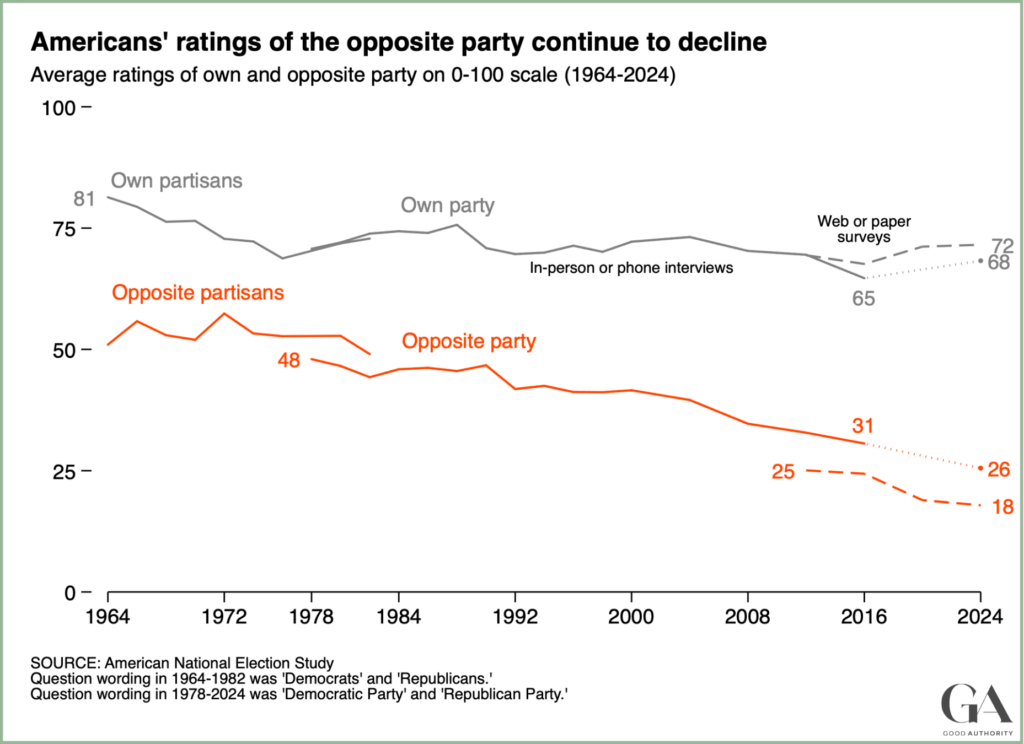
Problem 1: creates opportunity for “Texas Sharpshooter Fallacy”

“Fence” is case with outcome “high polarization”; “bullet holes” are attributes of that case

• can point to any attribute of the US and highlight as the “cause” (paint a bulls-eye)

Selection on the Dependent Variable

Problem 2: Causality is counterfactual. Outcome should be different when independent variable changes. Selecting on dependent variable: never observe outcome under different exposure to the “cause”.

• outcome (polarization) could have occurred without the alleged “cause” (social media). Without observing the counterfactual, we can’t rule this out.

Evidence for Causality

Causality is counterfactual: Need to observe the outcome/dependent variable in a case at different levels of the cause/independent variable.

\[\text{Polarization}_{USA} (\text{High Social Media Use}) = High \\ \color{red}{\text{Polarization}_{USA} (\text{Low Social Media Use}) = ?} \] but we can never observe the \(\color{red}{\text{counterfactual}}\)… \(\to\) Fundamental Problem of Causal Inference

Solving the FPCI?

If getting news from social media increased polarization

\(\color{red}{\mathrm{Polarization}_{USA}(\mathrm{Higher \ Social \ Media})} >\) \(\mathrm{Polarization}_{USA}(\mathrm{High \ Social \ Media}) >\) \(\color{red}{\mathrm{Polarization}_{USA}(\mathrm{Low \ Social \ Media})}\)

In order to provide evidence for causal claims, we need to find ways around the FPCI:

• We need to find something we can see that can stand in for the missing counterfactual

Social Media and Polarization

How could we observe “\(\color{red}{?}\)”, the unknown counterfactual?

• We could to find another country where there was lower social media use

Social Media and Polarization

We cannot observe: \(\color{red}{\mathrm{Polar.}_{USA}(\mathrm{Low \ S. M.})}\)

But we can observe, e.g.: \(\mathrm{Polar.}_{Germany}(\mathrm{Low \ S. M.})\)

If we assume:

\(\mathrm{Polar.}_{Germany}(\mathrm{Low \ S.M.})\) \(=\) \(\color{red}{\mathrm{Polar.}_{USA}(\mathrm{Low \ S.M.})}\)

Then, we can empirically test our causal claim

plugging in factual \(Germany\) for the counterfactual \(USA\)

48% of Americans report using social media for news. \(\mathrm{Polarization}_{USA}(\mathrm{Social \ Media \ News =48\% }) = 56\)

37% of Germans report using social media for news. \(\mathrm{Polarization}_{Germany}(\mathrm{Social \ Media \ News =37\% }) = 29\)

Solving the FPCI

Every solution to the FPCI involves:

1. Comparing the observed values of outcome \(Y\) in cases that factually have different values of cause \(X\)

2. Making assumption that factual (observed) potential outcomes from one case as equivalent to counterfactual (unobserved) potential outcomes of another case.

• The observed patterns of the association between the independent variable \(X\) and dependent variable \(Y\) we call correlations

Correlation

Correlation is the association/relationship between the observed/factual values of \(X\) (the independent variable) and \(Y\) (the dependent variable)

• loosely: describes the observed relationship between \(X\) and \(Y\).
• formally: mathematical definitions for specific kinds of associations.

Correlation

All empirical evidence for causal claims relies on correlation between the independent and dependent variables.

But, you’ve all heard this:

• Think how we filled in the \(\color{red}{\text{counterfactuals}}\) for the US: could anything go wrong?

Correlation

Many different ways of assessing correlation, but shared attributes:

• correlations have a direction:
  • positive: \(X\uparrow\), \(Y\uparrow\)
  • negative: \(X\uparrow\), \(Y\downarrow\)
• correlations have strength:
  • strong: \(X\) and \(Y\) almost always move together
  • weak: \(X\) and \(Y\) do not move together very much

Stronger

Weaker

Correlation

Many different ways of assessing correlation, but shared attributes:

• correlations have a direction:
  • positive: \(X\uparrow\), \(Y\uparrow\)
  • negative: \(X\uparrow\), \(Y\downarrow\)
• correlations have strength:
  • strong: \(X\) and \(Y\) almost always move together
  • weak: \(X\) and \(Y\) do not move together very much
• correlations have a magnitude:
  • how much \(Y\) changes with \(X\).

Correlation

Many ways of examining correlations:

• scatterplots (plot each case on an x-y coordinates)
• bar plots
• trends
• tables of coefficients

Scatterplot

Bar plot

Individual data on social media use and affective polarization from ANES 2024

Trend lines

Correlation

Formally…

common mathematical definition: correlation is the degree of linear association between \(X\) and \(Y\)

• Takes values between \(-1\) and \(1\)
• Values close to \(1\) or \(-1\) suggest strong degree of linear association
• Values close to \(0\) suggest weak degree of linear association
• Value of correlation does not tell us how much \(Y\) changes with \(X\) (no magnitude)

Correlation

What is it?

negative correlation: (\(< 0\)) values of \(X\) and \(Y\) move in opposite direction:

• higher values of \(X\) appear with lower values of \(Y\)
• lower values of \(X\) appear with higher values of \(Y\)

positive correlation: (\(> 0\)) values of \(X\) and \(Y\) move in same direction:

• higher values of \(X\) appear with higher values of \(Y\)
• lower values of \(X\) appear with lower values of \(Y\)

Correlation

Correlation

• It is possible to see perfect correlation but small (magnitude) change in \(Y\) across \(X\)

• It is possible to see weak correlation but large (magnitude) change in \(Y\) across \(X\)

• It is possible to see perfect nonlinear relationship between \(X\) and \(Y\) with \(0\) correlation

Correlation

weak correlation: values for \(X\) and \(Y\) do not cluster along line

strong correlation: values for \(X\) and \(Y\) cluster strongly along a line

strength of correlation does not determine the slope of line describing \(X,Y\) relationship

magnitude: this is the slope of the line describing the \(X,Y\) relationship. The larger the effect, the steeper the slope

Correlation: \(0.25\), Magnitude: \(0.23\). Does this correlation prove using social media for news causes polarization? Why or why not?

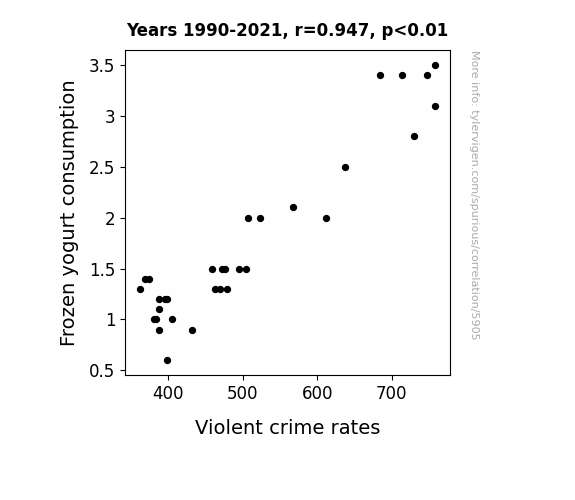
Correlation: 0.67, Magnitude: 5.82. Does this correlation prove that X caused drownings? Why or why not?

Correlation: 0.67, Magnitude: 5.82. Does this correlation prove that Nic Cage films caused drownings? Why or why not?

Two types of problems

• random association: correlations between \(X\) and \(Y\) occur by chance and do not reflect any systematic relationship between \(X\) and \(Y\). (In the extreme, absolutely no relationship between \(X\) and \(Y\))

• bias (spurious correlation, confounding): \(X\) and \(Y\) are correlated but the correlation does not result from causal relationship between those variables

Solving these problems involves making assumptions: what are those assumptions? how plausible are they?

Arbitrary processes can make seemingly-strong patterns.

If you look long enough at pure chaos, you might find a strong correlation

• It could have happened by chance!
• So an observed correlation might not mean any relationship (e.g. Nic Cage)

Arbitary Correlations

To see that random patterns can emerge, I use random number generators to

• randomly pick \(5\) values of \(X\) out of a “hat”
• randomly pick \(5\) values of \(Y\) out of a different “hat”

We can imagine these are the observed \(X\) and \(Y\) for \(5\) cases.

Could we find a strong correlation between \(X\) and \(Y\) (even if \(X\) and \(Y\) totally unrelated)?

• if it is easy, then evidence fails weak severity requirement
• if it is difficult, then it passes

\(\#\) Tries to get correlation \(> 0.9\): 22

What do we do about this problem?

• We can never rule out a chance correlation
• We can figure out how likely correlation occurred by chance.
• If chance correlation is very unlikely, then we set aside this concern (or indicate the “false positive rate” for this analysis)

How?

1. Compute correlation of \(X\) and \(Y\)
2. How strong is the correlation?
   • Patterns that are stronger are less likely to happen by chance
3. How many cases do we have?
   • Patterns with many cases are less likely to happen by chance
4. Assign a probability that observed correlation would have happened by chance, assuming claim is wrong (no correlation)

This procedure works…

Assuming…

1. we correctly describe the chance processes (save this for a stats class)
2. we don’t misuse our statistical tests

Tries to get correlation \(> 0.9\): 2134

Tries to get correlation \(> 0.9\): 452969

Tries to get correlation \(> 0.45\): 15

statistical significance:

An indication of how likely it is that correlation we observe could have happened purely by chance.

higher degree of statistical significance indicates correlation is unlikely to have happened by chance. (unlikely to observe evidence for the claim if claim is false)

\(p\) value:

• probability of observing this correlation, assuming truth is a \(0\) correlation between \(X\) and \(Y\).
• value between \(0\) and \(1\).
• Lower \(p\)-values indicate greater statistical significance

\(p < 0.05\) often used as threshold for “significant” result.

• but it is not a magic number
• we observe \(p < 0.05\) by chance (\(\frac{1}{20}\)th of the time)
• even if significant, magnitude of effect may be small

\(p\) value:

Advertised promise about weak severity:

if we use this correlation as evidence in support of a claim, what is probability of accepting the claim in error (due to random association)?

• only works if we don’t abuse the tests

\(p\) value:

Be wary of “\(p\)-hacking”/“snooping”

• \(p\) values become meaningless if we look at many correlations, then only report the ones that are “significant”.

Why?

Correlation: 0.67, \(p \le\) 0.025: 1 in 40 chance is easy to find when you look at 25 thousand possible correlations.

1. Correlations can appear by chance
2. We can assess probability of observing correlation by chance if we know:
   • strength of correlation (close to \(1,-1\))
   • size of the sample (\(N\))
   • we assume we know the chance process generating our observations
3. \(p\)-values:
   • Obtained using mathematical formulae
   • Given same \(N\), stronger correlation has lower \(p\)
   • Given same strength, correlation with more \(N\) has lower \(p\)

Correlation: 0.25, \(p \le\) 0.428

Does social media used cause polarization?

Correlation: 0.07, \(p \le\) 0.0000020

Does social media used cause polarization?

\(1.\) Correlation as “solution” to Fundamental Problem of Causal Inference

\(2.\) Correlation suffers from two problems:

• Random Association: assess \(p\) values and statistical significance, based on assumptions about chance process
• Bias: we call this “confounding”, more on Thursday